|
cosnavi.jp |
| ���w�Z�@�w�K�w���v�� �y����z |
| ���w�� |
| ��R�́@�e�w�N�̖ڕW�y�ѓ��e |
| ��Q�߁@��Q�w�N�̖ڕW�y�ѓ��e |
| �Q�@��Q�w�N�̓��e |
| �a�@�}�` |
| �a (2) �}�`�̍��� |
| ���w�Z�@�w�K�w���v�� �y�{���z |
�i2�j �}�`�̍����ɂ��āC���w�I������ʂ��āC���̎�����g�ɕt���邱�Ƃ��ł���悤�w������B -------------------------------- �A�@���̂悤�Ȓm���y�ыZ�\��g�ɕt���邱�ƁB �i��j ���ʐ}�`�̍����̈Ӗ��y�юO�p�`�̍��������ɂ��ė������邱�ƁB �i��j �ؖ��̕K�v���ƈӖ��y�т��̕��@�ɂ��ė������邱�ƁB -------------------------------- �C�@���̂悤�Ȏv�l�́C���f�́C�\���͓���g�ɕt���邱�ƁB �i��j �O�p�`�̍��������Ȃǂ���ɂ��ĎO�p�`�╽�s�l�ӌ`�̊�{�I�Ȑ�����_���I�Ɋm���߂���C�ؖ���ǂ�ŐV���Ȑ����������������肷�邱�ƁB �i��j �O�p�`�╽�s�l�ӌ`�̊�{�I�Ȑ����Ȃǂ���̓I�ȏ�ʂŊ��p���邱�ƁB |
�k�p��E�L���l �@�@��`�@�ؖ��@�t�@����@≡ |
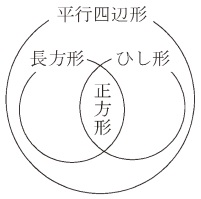
�m���e�̎戵���n �i1�j ���e�́u�a�}�`�v�́i2�j�̃C�́i��j�Ɋ֘A���āC�����`�C�Ђ��`�y�ђ����`�����s�l�ӌ`�̓��ʂȌ`�ł��邱�Ƃ���舵�����̂Ƃ���B |
| ���w�Z�@�w�K�w���v�� �y����z |
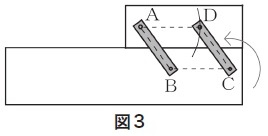
�@�i1�j�ł́C���ʐ}�`�̊p�Ɋւ��鐫�����C���s���̐������g���ē����C��������ɂ��ċؓ����Ăčl���������邱�Ƃ��o�������B �@�����ł́C�X�ɎO�p�`�̍����������g���āC�}�`�̐��������(����)�I�Ɋm���߁C�_���I�ɍl�@���\������͂�{�����Ƃ��˂炢�Ƃ��Ă���B -------------------------------- �@���w�Z�Z���Ȃɂ����āC��R�w�N�ł͓ӎO�p�`�̐����ɂ��āC�܂��C��S�w�N�ł͕��s�l�ӌ`�̐����ɂ��āC���ꂼ��}�`�̊p��ӂɒ��ڂ��C�����C�����C�ώ@�Ȃǂɂ���Ē��ׂĂ��Ă���B -------------------------------- �@���w�Z��Q�w�N�ł́C���w�I�ɐ��_���邱�Ƃɂ���āC�}�`�̐����ׂ邱�Ƃ��ł���悤�ɂ���B �@����ɁC���ׂ�ߒ��₻�̌��ʂɂ��Đ������`������������ʂ��āC�K�ɕ\���ł���悤�ɂ���B |
| �֘A�ꏊ�փW�����v |
| → ���w�Z���w�� �ڎ� |
| → ���w�Z�Z���� �ڎ� |
| → ���w�Z�w�K�w���v�́i2017�j�ڎ� |
| → �w�K�w���v�̃i�r �g�b�v�y�[�W |