（1） 一次関数について，数学的活動を通して，次の事項を身に付けることができるよう指導する。

--------------------------------

ア　次のような知識及び技能を身に付けること。

（ｱ） 一次関数について理解すること。

（ｲ） 事象の中には一次関数として捉えられるものがあることを知ること。

（ｳ） 二元一次方程式を関数を表す式とみること。

--------------------------------

イ　次のような思考力，判断力，表現力等を身に付けること。

（ｱ） 一次関数として捉えられる二つの数量について，変化や対応の特徴を見いだし，表，式，グラフを相互に関連付けて考察し表現すること。

（ｲ） 一次関数を用いて具体的な事象を捉え考察し表現すること。

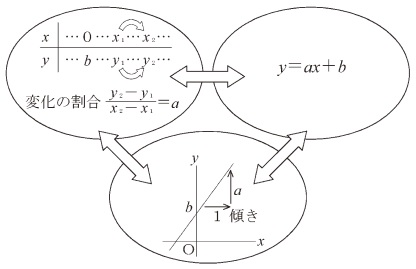
〔用語・記号〕　　変化の割合　傾き

　第１学年では，具体的な事象における二つの数量の変化や対応を調べ，関数関係について理解し，比例，反比例を関数として捉え直した。

　そこでは，変数と変域や座標について理解するとともに，比例，反比例の関係を表，式，グラフなどで表し，それらを関連付けながら変化や対応の特徴を考察することや，比例，反比例を用いて具体的な事象を捉え考察し表現することを学習している。

--------------------------------

　第２学年では，第１学年と同様に具体的な事象における二つの数量の変化や対応を調べることを通して，一次関数について考察する。

　これらの学習を通して，関数関係を見いだし考察し表現することができるようにする。

--------------------------------

　一次関数の学習は比例の学習の発展である。

　同時に，変化の割合に着目するなど，文字を用いた式によって関数をより深く学習する入り口ともなっている。

　第２学年では，比例，反比例の学習を基に，一次関数について理解し，関数関係についての理解を深める。

--------------------------------

　具体的な事象の中から関数関係にある二つの数量x，y を取り出し，それらの変化や対応を調べることを通して，それらの間に，次のような関係があることを見いだす。

・ x の値がk 増えるに従い，y の値がak 増える。

--------------------------------

　このような学習の上に立って，その関係を文字を用いた式で表現する。

　こうして，一次関数が，一般的に，a，b を定数として，y＝ax＋b という式で表される関係であることを理解する。

　そして，事象の中には一次関数を用いて捉えられるものがあることを知る。

--------------------------------

　第１学年における比例，反比例の学習の上に立って，具体的な事象について伴って変わる二つの数量を取り出し，それらの間にどのような関数関係があるか，また，それがどのような式やグラフで表されるかなどを考察する。

　比例関係は，一次関数 y＝ax＋b の特別な場合である。

　二元一次方程式 ax＋by＋c＝０を，
　二つの変数x とy の間の関係
　を表した式とみれば，
　この条件を満たすx とy の値の組が
　考察の対象となる。

　この式で
　x とy の値の組を求める場合，

　b≠０のとき，
　x のとる値を一つ決めれば，
　それに対応して y の値が一つ決まる
　ことが分かり，

　このことから，
　ax＋by＋c＝０は，
　x とy の間の関数関係を表す式
　とみることができる。

--------------------------------

　例えば，

　二元一次方程式 x−２y＋６＝０は，
　x とy の間の関数関係を表す式
　とみることができ，
　またこの式を，

　と変形することによって，
　y はx の一次関数であることが分かる。

　さらに，
　二元一次方程式のグラフが
　直線となることから，
　連立二元一次方程式の解は
　座標平面上の２直線の交点の座標
　としても求められる。

　グラフを用いることにより，
　連立二元一次方程式の解の意味を
　視覚的に捉えて理解することができる。

　第１学年では，生徒自らが関数関係にある二つの数量を取り出し，表，式，グラフを用いてそれらの変化や対応に関する特徴を考察し表現することについて学習している。

　第２学年では，これらの学習の上に立って，一次関数の特徴を表，式，グラフで捉えるとともに，それらを相互に関連付けることで，一次関数についての理解を深める。

--------------------------------

　これまでは，関数の変化の仕方を捉える際に，表を基にして対応する数量の比を考えたり，増加するか減少するかを考えたりしてきた。

　一次関数の変化の仕方については，更に明確に捉えるために，x の増加量に対するy の増加量の割合である変化の割合について学習する。

--------------------------------

　一次関数y＝ax＋b について，
　変数x の値が
　x1 からx2 まで変化すると，
　それに伴って変数y の値も
　y1 からy2 まで変化するものとする。

　このとき，変化の割合

　は，常に一定でa に等しい。

　これは，一次関数の特徴であって，
　グラフが直線になることを意味している。

--------------------------------

　このような
　変化の割合についての考察を通して，

　x の係数a は，
　x の値が１だけ増加したとき，
　対応するy の値がどれだけ増加するか
　を表していること，

　さらに，
　x の値の増加に対しての
　y の値の増加分も，
　a の値を基にして求められること

　などを理解できるようにする。

--------------------------------

　一次関数 y＝ax＋b のグラフは直線であり，a は直線の傾きを決めるものであるから，y のとる値の増減については，傾きa の正，負によって判断できる。

　また，b はx＝０に対応するy の値であり，それは，グラフとy軸との交点のy座標であることも理解できるようにする。

★↑画像をクリックすると拡大します！

--------------------------------

　なお，変化の割合を指導する際には，形式的に変化の割合を計算して求めることに偏らないようにするとともに，変化の割合を事象の考察やその表現に適切に用いることができるようにすることが大切である。

　第１学年でも指導したように，日常の事象や社会の事象及び数学の事象には，関数関係として捉えられるものが数多く存在する。

　ここでは，一次関数を用いて具体的な事象を捉え考察し表現することを指導する。

　事象を捉え考察し表現する際には，何を明らかにしようとするかという目的意識をもち，事象をどのように捉え，数学の対象にするのかを明確にした上で数学的に表現した問題を見いだすことが求められる。

　その上で問題を解決する際には，目的に応じて表，式，グラフを適切に選択し的確に表現することが大切である。

--------------------------------

　具体的な事象の中から観察や操作，実験などによって取り出した二つの数量について，事象を理想化したり単純化したりすることによって，それらの関係を一次関数とみなし，そのことを根拠として変化や対応の様子を考察したり予測したりすることができる。

　例えば，水を熱した時間と水温の関係を調べる際，実験を基にグラフを作成して考察する。

　ここで，実験によるデータの点がグラフでほぼ一直線上に並んでいることを基にして，一定の熱量で加熱しているなどと理想化したり，熱した時間だけで水温が決まると事象を単純化したりすることによって，二つの数量の関係を一次関数とみなす。

　その上で，一次関数を式に表し，それを基にして水がある温度になるまでの時間を予測し，その根拠を説明する。

　また，実験の結果と予測を比較・検討し，伝え合う活動を通して，結果と予測に違いがある原因について考えたり，よりよい予測のための手立てを工夫したりすることもできる。

--------------------------------

　なお，関数として考察することによって，他の領域において学習する内容についての理解を深めることもできる。

　例えば，図形の領域において学習するn 角形の内角の和を求めるときに，n が増えていくときの内角の和の増え方を関数として考察すると，変化の割合が180 であることから，多角形の頂点が一つ増えると，三角形一つ分の内角の和が増えていることが分かる。