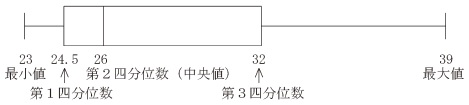
（1） データの分布について，数学的活動を通して，次の事項を身に付けることができるよう指導する。

--------------------------------

ア　次のような知識及び技能を身に付けること。

（ｱ） 四分位範囲や箱ひげ図の必要性と意味を理解すること。

（ｲ） コンピュータなどの情報手段を用いるなどしてデータを整理し箱ひげ図で表すこと。

--------------------------------

イ　次のような思考力，判断力，表現力等を身に付けること。

（ｱ） 四分位範囲や箱ひげ図を用いてデータの分布の傾向を比較して読み取り，批判的に考察し判断すること。

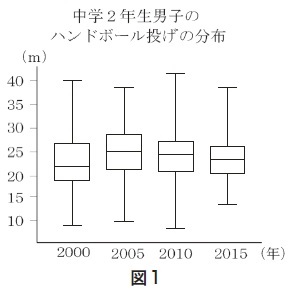
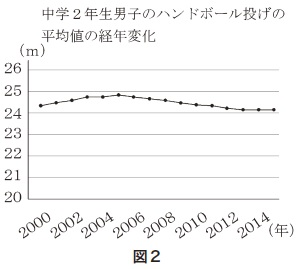
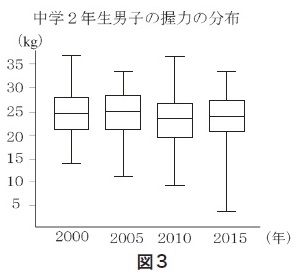
　第１学年では，ヒストグラムや相対度数などについて学習している。

　第２学年では，これに加えて四分位範囲や箱ひげ図を学習することで，複数の集団のデータの分布に着目し，その傾向を比較して読み取り，批判的に考察して判断する力を養う。

　第１学年では，量的データの分布を捉える方法として，ヒストグラムや相対度数などについて学習している。

　ヒストグラムは分布の形は分かりやすい一方で，中央値などの指標が分かりづらい。

　複数のデータの分布を比較する際に，視覚的に比較がしやすい統計的な表現として，箱ひげ図がある。

--------------------------------

　箱ひげ図とは，次のように，最小値，第１四分位数，中央値（第２四分位数），第３四分位数，最大値を箱と線（ひげ）を用いて一つの図で表したものである。

　四分位数とは，全てのデータを小さい順に並べて四つに等しく分けたときの三つの区切りの値を表し，小さい方から第１四分位数，第２四分位数，第３四分位数という。

　第２四分位数は中央値のことである。

　なお，四分位数を求める方法として幾つかの方法が提案されているが，ここでは四分位数の意味を把握しやすい方法を用いる。

--------------------------------

　例えば，次の九つの値があるとき，中央値（第２四分位数）は５番目の26 である。

　23　24　25　26　26　29　30　34　39

　この５番目の値の前後で二つに分けたときの，１番目から４番目までの値のうちの中央値24.5 を第１四分位数，６番目から９番目までの値のうちの中央値32 を第３四分位数とする。

★↑画像をクリックすると拡大します！

　箱ひげ図の箱で示された区間に，全てのデータのうち，真ん中に集まる約半数のデータが含まれる。

　この箱の横の長さを四分位範囲といい，第３四分位数から第１四分位数を引いた値で求められる。

　上の例では四分位範囲は32−24.5＝7.5 である。

　四分位範囲はデータの散らばりの度合いを表す指標として用いられる。

　極端にかけ離れた値が一つでもあると，最大値や最小値が大きく変化し，範囲はその影響を受けやすいが，四分位範囲はその影響をほとんど受けないという性質がある。

　また，この図中に，平均値を記入して中央値との差を考えたり，第１四分位数や第３四分位数と中央値との差を考えたりすることにより，データの散らばり具合が把握しやすくなるので，複数のデータの分布を比較する場合などに使われる。

　四分位範囲や箱ひげ図を用いて，複数の集団のデータの分布の傾向を比較して読み取り，批判的に考察したり判断したことを説明したりすることができるようにする。

--------------------------------

　指導に当たっては，日常の事象を題材とした問題などを取り上げ，それを解決するために必要なデータを収集し，コンピュータなどを利用してデータを整理し，四分位範囲を求めたり箱ひげ図で表したりして複数の集団のデータの傾向を比較して読み取り，その結果を基に説明するという一連の活動を経験できるようにすることが重要である。

　例えば，中学生の体力は以前に比べて落ちているといえるかどうかについて考える。

　データとしては，生徒にとっての考察のしやすさから，同じ学校の中学校２年生男子の体力テストの結果を用いることができるであろう。

　そこで，ハンドボール投げに焦点化し，2000年，2005年，2010年，2015年のデータから箱ひげ図（図１）を作成するなどして分布の傾向を比較して読み取り，これを基に，「中学生の体力は前に比べて落ちているといえるかどうか」について考察する。

　具体的には，「四分位範囲を表す箱は，2005年からそれほど大きく下がっておらず，中央値を中心とする全体の約半数のデータはそれほど下がっているわけではないので，体力が落ちているとは言えない」と判断することが考えられる。

　ここで，より詳しく検討するために，範囲の違いに着目して，2010年と2015年に絞ってヒストグラムを作成し，これらの分布を詳しく比較することが考えられる。

　それにより，かけ離れた値があるかどうかなど，範囲が大きく異なる理由について検討することができる。

　また，５年ごとではなく毎年の中央値や平均値などに着目して折れ線グラフ（図２）を作成することで，経年変化の様子を調べることができる。

　さらに，「ハンドボール投げのデータだけで十分か」と批判的に考え，握力など他の体力テストのデータから箱ひげ図（図３）やヒストグラムを作成するなどして，一層詳しい考察を加えることも考えられる。

--------------------------------

　このように，体力に対して多様なデータや統計的な表現を用いて多面的に吟味することで，批判的に考察することの必要性に気付くことが大切である。

　また，データの傾向を捉える場合，日常生活では，簡潔さの観点から箱ひげ図のみを用いて説明することが予想される。

　しかし，そのことによって分布の形など，失われる情報もあるので，必要に応じてヒストグラムなどと合わせて用いることが必要な場面もあることに留意する。

　なお，同じ学校のデータについての判断の結果を，中学生一般について考察することは，第３学年で学習する標本調査に関わることである。