（1） 「Ａ数と式」，「Ｂ図形」，「Ｃ関数」及び「Ｄデータの活用」の学習やそれらを相互に関連付けた学習において，次のような数学的活動に取り組むものとする。

ア　日常の事象や社会の事象を数理的に捉え，数学的に表現・処理し，問題を解決したり，解決の過程や結果を振り返って考察したりする活動

イ　数学の事象から見通しをもって問題を見いだし解決したり，解決の過程や結果を振り返って統合的・発展的に考察したりする活動

ウ　数学的な表現を用いて論理的に説明し伝え合う活動

　第１学年においては，

　各領域の学習や
　それらを相互に関連付けた学習
　において，

　「日常の事象を数理的に捉え，
　　数学的に表現・処理し，
　　問題を解決したり，
　　解決の過程や結果を
　　振り返って考察したりする活動」，

　「数学の事象から
　　問題を見いだし解決したり，
　　解決の過程や結果を振り返って
　　統合的・発展的に考察したりする
　　活動」，

　「数学的な表現を用いて
　　筋道立てて説明し伝え合う活動」

　に取り組む機会を設けることで，

　生徒が
　数学的活動に主体的に取り組み，
　基礎的・基本的な知識及び技能を
　確実に身に付けるとともに，
　思考力，判断力，表現力等を高め，
　数学を学ぶことの楽しさや意義を
　実感できるようにすること
　を目指している。

--------------------------------

　第２学年では，こうした基本的な考えを一層重視するとともに，生徒の発達の段階や学習の状況，第２学年で指導する各領域の内容との関係を考慮し，数学的活動の質を高めていく。

　なお，提示されている三つの活動は第３学年と同じである。

　これは，当該学年で指導する内容に即し，２年間をかけて継続した指導をすることが必要であると判断したためである。

　第１学年における

　「日常の事象を数理的に捉え，
　　数学的に表現・処理し，
　　問題を解決したり，
　　解決の過程や結果を
　　振り返って考察したりする活動」

　は，生徒にとって身近なできごとなどを
　考察の対象として，
　数学を利用することを重視している。

　第２学年においては，
　数学を利用する範囲を広げ，
　社会における様々な事象なども
　視野に入れて
　活動に取り組む機会を設ける。

--------------------------------

　数学を利用する範囲を広げ，直接体験できないことについても自分のこととして考えながら活動に取り組むなどして，数学的活動の楽しさや数学のよさを実感できるようにすることが大切である。

--------------------------------

　なお，各領域の内容との関係を考慮して数学を利用する対象を適切に定め，この活動の趣旨が実現されるようにすることが大切である。

--------------------------------

　第２学年における

　「日常の事象や社会の事象を
　　数理的に捉え，
　　数学的に表現・処理し，
　　問題を解決したり，
　　解決の過程や結果を
　　振り返って考察したりする活動」

　として，
　例えば次のような活動が考えられる。

　この活動は，第２学年「Ｃ関数」の（1）のイの（ｲ）「一次関数を用いて具体的な事象を捉え考察し表現すること」の指導における数学的活動であり，

　例えば，８月に富士山の６合目まで登る予定を立て，服装を準備するために，「８月の６合目付近の高さの気温はどれくらいだろうか」という日常の事象の問題を取り上げる。

　この問題を解決するために，入手できる幾つかの観測地点の気温に関するデータを基に，８月の６合目付近の高さの気温を予測することをねらいとする。

　また，その過程において，事象を理想化したり単純化したりすることで，実験や観察による数量の関係を一次関数とみなし，表，式，グラフを用いて表現・処理し，それを基に予測できることのよさを知り，様々な事象の考察に生かすことができるようにする。

--------------------------------

　この活動に生徒が主体的・対話的に取り組むことができるようにし，深い学びの実現につなげることが大切である。

　そのために，一次関数の特徴を，表，式，グラフで捉えるとともに，それらを相互に関連付け，一次関数について理解できるよう指導とその計画を工夫する。

　また，事象を理想化したり単純化したりすることで，数量の関係を一次関数とみなすことの意味を，例えば，線香に火をつけてから燃え尽きるまでの時間を予測するなどの事例を基に理解できるような機会を設ける。

　その際，数量の関係を一次関数とみなして考察するときには，一定の制約が生じることについても理解できるようにする。

--------------------------------

　こうした指導を踏まえ，富士山の６合目付近の高さの気温を予測する活動に取り組む機会を設ける。

　まず，８月の富士山周辺地点や富士山の山頂地点の平均気温のデータを調べて表やグラフに表す。

　次に，変化の割合がほぼ同じであることや，グラフの点がほぼ一直線上に並んでいることなどを基に，気温が高さの一次関数であるとみなし，それらの点を基に直線を引いたり，表の中の数値を基に一次関数の式で表したりする。

　このことで，富士山の６合目付近の高さの気温を予測する。

　その際，グラフには，おおよその数値を読み取ることができるというよさがあるものの，グラフの直線の引き方によって予測した気温が異なる場合があることや，数値を用いて計算で求めるためには，高さと気温の関係を式で表すとよいことなど，解決の過程や結果を振り返って，表，式，グラフのそれぞれのよさについて検討する機会を設けることも大切である。

　また，一次関数とみなしているのはある変域においてのことであることや，一次関数とみなすことに無理のある事象があることにも触れ，日常の事象や社会の事象から一次関数とみなすことで解決できる問題を考察する際に生かせるようにする。

　数学科において主体的・対話的で深い学びを実現するためには，問題を解決することと同様に，見通しをもって問題を発見することにも焦点を当てることが求められる。

　第１学年における「数学の事象から問題を見いだし解決したり，解決の過程や結果を振り返って統合的・発展的に考察したりする活動」は，数学の事象から数学的に表現した新たな問題を見いだし，既習の内容を活用してそれを解決し，その過程や結果を振り返ることで概念を形成したり，新たなものを見いだしたりする過程を重視している。

　このことを踏まえ，第２学年においては，第１学年で経験した問題発見・解決の過程について，更に見通しをもって遂行できるようにすることを重視する。

--------------------------------

　数学的活動の過程では，各領域の内容の高まりとともに，演繹(えき)による検証の必要性や数学的な推論を適切に用いて新たな事柄を見いだすことの重要性が増してくる。

　このため，帰納や類推（予測や推測の構成）や演繹(えき)（正しさの確認や検証）などの数学的な推論の進め方の質を高め，より洗練されたものにしていくことが大切である。

--------------------------------

　見いだした数や図形の性質などから統合的・発展的に考察するためには，例えば，仮定や結論に目を向けて，条件をかえたり，逆を考えたりするなどの見通しをもって問題を見いだすことが必要になる。

　また，これまで進めてきた数学的な推論がそのきっかけになることにも留意する必要がある。

--------------------------------

　第２学年における「数学の事象から見通しをもって問題を見いだし解決したり，解決の過程や結果を振り返って統合的・発展的に考察したりする活動」として，例えば次のような活動が考えられる。

　この活動は，第２学年「Ｂ図形」の（1）のイの（ｱ）「基本的な平面図形の性質を見いだし，平行線や角の性質を基にしてそれらを確かめ説明すること」の指導における数学的活動である。

　ここでのねらいは，多角形の内角や外角に関する事象から，n角形の内角の和180ﾟ×（n−２）及び外角の和360ﾟについての問題を見いだし，既習の図形の性質などを用いて解決し，その過程や結果について統合的・発展的に考察することとする。

　このことによって既習の内容に結び付けて考えることのよさを知ったり，新たな問題が見いだせることに気付いたりできるようにして，その後の図形の学習などに生かすことができるようにする。

--------------------------------

　この活動に生徒が主体的・対話的に取り組むことができるようにし，深い学びの実現につなげることが大切である。

　そのために，多角形を一つの頂点から引いた対角線で三角形に分割する（図１）ことで，n角形の内角の和が180ﾟ×（n−２）になることを理解できるよう指導とその計画を工夫する。

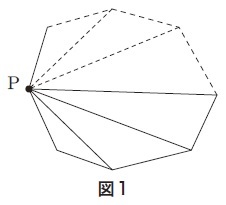
　その際，
　三角形，四角形などの内角の和を
　帰納的に調べ，
　そこには規則性がありそうなことに
　気付き，
　これまでに学習してきたことを基に，
　「多角形の内角の和は
　　式に表すことができそうだ」
　などの見通しをもって
　問題として表現することが
　できるようにする。

　また，
　見いだした内角の和を表す式が
　正しいといえるかどうかについては，

　「多角形を三角形に分割すればよい」，

　「三角形の内角の和が180ﾟであることを
　　証明の根拠にすればよい」

　などを明らかにし，

　「n角形の内角の和が
　　180ﾟ×（n−２）になる」ことを
　説明する機会を設ける

　など指導の計画を工夫する。

--------------------------------

　こうした指導を踏まえ，多角形を三角形に分割する仕方に着目して，内角の和を求める他の方法を考察し表現する活動に取り組む機会を設ける。

　例えば，多角形の辺上の１点から各頂点に引いた線分で三角形に分割する（図２）ことや，

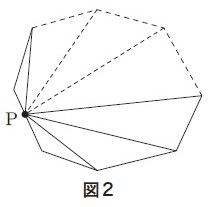
　多角形の内部の１点から各頂点に引いた線分で三角形に分割する（図３）ことから，

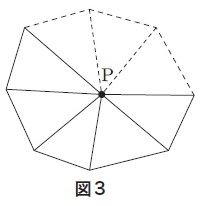
　三角形の内角の和が180ﾟであることを証明の根拠にしてn角形の内角の和を表す式を導くことが考えられる。

--------------------------------

　これらの求め方について考察した後，
　それらの方法を比較し，

　「多角形を三角形に分割していること」，

　「三角形の内角の和が180ﾟであること
　　を証明の根拠にしていること」

　などの共通点や相違点に
　気付くことができるよう促す。

　さらに，
　共通する考え
　「三角形に分割して
　　内角以外の角は除けばよい」
　で三つの求め方を統合すること
　も考えられる。

--------------------------------

　次に，多角形の外角に着目し，その和について問題を見いだすことができる。（図４）

--------------------------------

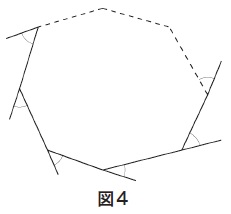
　ここでは，四角形や五角形などの外角の和を帰納的に調べ，

「どんな多角形でも外角の和は360ﾟになるのではないか」

　という推測から問題を設定し，

「一つの頂点で内角と外角の和が180ﾟになることを使えばよい」

などの見通しをもち，その説明を考えることもできる。

　第１学年における「数学的な表現を用いて筋道立てて説明し伝え合う活動」は，表現の簡潔さや形式などにとらわれ過ぎず，生徒が筋道立てて説明し伝え合うことを重視している。

　第２学年においては，それらが洗練され，より実質的なものになるように，根拠を明らかにし論理的に説明し伝え合う活動に取り組む機会を設ける。

--------------------------------

　数学の学習においては，学年が進むとともに，前提と結論を明示して見いだしたことを的確に伝えること，計算の手順や方程式を解く方法などを順序よく分かりやすく示すこと，見いだしたことの正しさや妥当性について根拠を明らかにして説明することなどの必要性が増し，論理的に説明し伝え合うことの重要性も高まる。

--------------------------------

　また，数学的な表現を用いることに関して，数量や図形などに関する事実や処理の仕方，思考の過程や判断の根拠などを数学的に表現したり，表現されたものを解釈したりすることの適切さを高めるためには，言葉や数，式，図，表，グラフなどを相互に関連付けて適切に用いることが重要になる。

　特に，数学的な表現を用いて伝え合う際には，相手に理解されやすくなるように説明することが重要であることを理解し，数学的に表現することのよさを実感できるようにする。

--------------------------------

　第２学年においては，思考の過程や判断の根拠などを数学的に表現するために，数学的な推論とその過程について理解し，これらを適切に用いることを重視する。

--------------------------------

　第２学年における「数学的な表現を用いて論理的に説明し伝え合う活動」として，例えば次のような活動が考えられる。

　この活動は，第２学年「Ｄデータの活用」の（2）のイの（ｲ）「確率を用いて不確定な事象を捉え考察し表現すること」の指導における数学的活動である。

　ここでのねらいは，例えば「くじ引きをするとき，先に引くか，後に引くか，どちらでもよいか」について判断を求め，その理由について確率を用いて説明することとする。

　またその過程において，求めた確率に基づいてどのような判断ができるのかを知り，不確定な事象の考察に生かせるようにする。

--------------------------------

　この活動に生徒が主体的・対話的に取り組むことができるようにし，深い学びの実現につなげることが大切である。

　そのために，多数回の試行をしたり，起こり得る場合の数を求めたりして簡単な場合について確率を求めることができるよう指導とその計画を工夫する。

--------------------------------

　こうした指導を踏まえ，くじ引きが公平であるかどうかを説明する活動に取り組む機会を設ける。

　まず，くじを引く順序によって当たりやすさに違いがあるかどうかについて「先に引いた方が当たりやすい」，「後から引いた方が当たりやすい」，「どちらも同じ」など直観的に予想を立てる。

　その上で，例えば「５本のうち２本の当たりくじが入っているくじを２人の生徒が引くとき，引く順番によって当たりやすさに違いがあるか」と問題を焦点化する。

　実際に何回かくじ引きを行うなどして試行の結果からも予想を立てておくようにするとよい。

　次に，予想が正しいかどうかを調べるために，樹形図などを作って起こり得る場合の数を求め，先に引いた場合と後から引いた場合で当たる確率をそれぞれ計算する。

　この場合，どちらの確率も2/5 となり，確率が等しいことから「引く順序によって当たりやすさに違いがない」と判断し，くじ引きが公平である理由を説明する。

　その際，各自の説明を他者のものと比較し，不十分な点を指摘し合うなどして，協働的に表現を洗練することが考えられる。

　確率を求めることができても説明することができない生徒には，確率の意味を見直すように促す。

--------------------------------

　また，焦点化された問題について，「問題の条件を変えても当たりやすさに違いはないか」と発展的に考え，新たな問題を見いだすことができる。

　例えば「４本のうち２本の当たりくじが入っているくじを３人の生徒で引くとき，何番目に引いても確率は1/2 になるか」など，くじの総数や当たりくじの本数，人数を変えてもくじ引きが公平であるかどうかについて，生徒の疑問に従って自立的に説明し，レポートにまとめ発表する機会を設けることも考えられる。