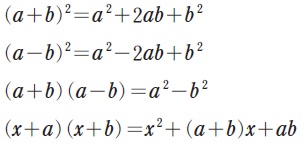（2） 簡単な多項式について，数学的活動を通して，次の事項を身に付けることができるよう指導する。

--------------------------------

ア　次のような知識及び技能を身に付けること。

（ｱ） 単項式と多項式の乗法及び多項式を単項式で割る除法の計算をすること。

（ｲ） 簡単な一次式の乗法の計算及び次の公式を用いる簡単な式の展開や因数分解をすること。

--------------------------------

イ　次のような思考力，判断力，表現力等を身に付けること。

（ｱ） 既に学習した計算の方法と関連付けて，式の展開や因数分解をする方法を考察し表現すること。

（ｲ） 文字を用いた式で数量及び数量の関係を捉え説明すること。

〔用語・記号〕　　因数

　第２学年では，文字を用いて数量の関係や法則などを考察する力を養うとともに，簡単な整式の加法・減法，単項式の乗法と除法の計算について学習している。

　また，数量や数量の関係を捉え説明するのに文字を用いた式が活用できることや，目的に応じて簡単な式を変形することについて学習している。

--------------------------------

　第３学年では，これらの学習の上に立って，単項式と多項式の乗法，多項式を単項式で割る除法及び簡単な一次式の乗法の計算ができるようにする。

　さらに，公式を用いる簡単な式の展開と因数分解を取り扱い，これによって，文字を用いた式で数量及び数量の関係を捉え説明する力を養うようにする。

　単項式の乗法と除法，
　数と多項式の乗法，
　多項式を数で割る除法については，
　既に学習している。

　これらの学習を基にして，
　第３学年では，
　例えば，

　２a×（３a−５b）
　のような単項式と多項式の乗法，

　（４x²＋６x）÷２x
　のような多項式を単項式で割る除法

　について学習する。

--------------------------------

　特に，単項式と多項式の乗法は，多項式の乗法の前段階として位置付けられるので，技能の確実な習得について十分な配慮が必要である。

　一次式と一次式の乗法では，既習の単項式と多項式の乗法と関連付けて考察し，単に形式的に計算ができるようにするだけではなく，その方法が交換法則，結合法則や分配法則などを基にしていることを理解できるようにすることが大切である。

　例えば，
　（a＋b）（c＋d）を展開するのに
　式 a＋b を一つの文字M に置き換えて，
　M（c＋d）＝Mc＋Md
　とすることで，
　既習の法則を用いて
　計算することができるようになる
　ことが分かる。

--------------------------------

　また，
　式の展開の公式としては，
　次のものを取り扱う。

　これらは，
　今後の学習において
　しばしば活用される
　典型的なものであり，
　公式のもつ意味を理解し，
　式を能率よく処理することが
　できるようにする。

--------------------------------

　因数分解の公式は，一次式の乗法や式の展開の公式の逆であることを理解し，その方法を見いだすことができるようにする。

--------------------------------

　また，式の展開の公式や因数分解の方法の理解を深めるために数の計算と関連付けて，そのよさを実感できるようにする。

　例えば，

　や

　を用いて
　下のように計算することが考えられる。

--------------------------------

　なお，ここで取り上げる式の展開や因数分解は，数や図形の性質が成り立つことを，文字を用いた式で説明したり，二次方程式を解いたりする程度の式の計算であり，必要以上に複雑で無目的な計算練習にならないようにする。

　乗法公式や因数分解の公式は，数や図形の性質などが成り立つことを，文字を用いた式を使って説明したり，二次方程式を解いたりする場合にしばしば活用される。

　したがって，これらの公式を能率的に活用し，目的に応じて式を変形したり式の意味を読み取ったりできるようになることが重要である。

　第２学年における指導を踏まえ，文字を用いた式で数量及び数量の関係を捉え説明することができるようにし，文字を用いた式を使うことのよさや必要性についての理解を一層深める。

　例えば，「連続する二つの偶数の積に１をたすと，奇数の２乗になる」ことを説明する場合，その過程は概(おおむ)ね次のようになる。

�@ 小さい方の偶数を自然数を表す文字n を用いて２n とすると，大きい方の偶数は２n＋２と表すことができる。

�A 「連続する二つの偶数の積に１をたす」ことは，２n（２n＋２）＋１を計算することを意味する。

�B その計算結果が「奇数の２乗になる」ことを示したいのだから，

　２n（２n＋２）＋１を（奇数）²
　という形の式に変形すること
　を目指す。

--------------------------------

　こうした方針を明らかにした上で
　具体的な式変形の過程を
　示し説明することで，
　「連続する二つの偶数の積に
　　１をたすと，
　　奇数の２乗になる」
　理由が伝わりやすくなる。

　ここで説明とは，
　単に説明が書けること
　だけを意味するものではなく，
　その内容を，
　簡潔・明瞭・的確に表現し
　相手に分かりやすく伝えること
　も意味する。

--------------------------------

　また，この学習では，

　　２n（２n＋２）＋１＝（２n＋１）²

　という式の変形を振り返り，
　２n＋１が，
　連続する偶数２n と２n＋２の間の奇数
　であることから，

　「連続する二つの偶数の積に
　　１をたすと，
　　二つの偶数の間にある奇数の２乗
　　になる」
　とその意味を読み取ることもできる。

　これは，
　第２学年の「Ｂ図形」の領域における
　「証明を読んで
　　新たな性質を見いだすこと」
　と関わる内容であり，
　統合的・発展的に考える力を養うこと
　につながる。