|
cosnavi.jp |
| ���w�Z�@�w�K�w���v�� �y����z |
| �Z���� |
| ��R�́@�e�w�N�̓��e |
| ��T�߁@��T�w�N�̖ڕW�y�ѓ��e |
| �Q�@��T�w�N�̓��e |
| �`�@���ƌv�Z |
| �`�i3�j�����̏�@�C���@ |
| ���w�Z�@�w�K�w���v�� �y�{���z |
�i3�j �����̏�@�y�я��@�Ɋւ�鐔�w�I������ʂ��āC���̎�����g�ɕt���邱�Ƃ��ł���悤�w������B -------------------------------- �A�@���̂悤�Ȓm���y�ыZ�\��g�ɕt���邱�ƁB �i��j �搔�⏜���������ł���ꍇ�̏����̏�@�y�я��@�̈Ӗ��ɂ��ė������邱�ƁB �i��j �����̏�@�y�я��@�̌v�Z���ł��邱�ƁB �@�܂��C�]��̑傫���ɂ��ė������邱�ƁB �i��j �����̏�@�y�я��@�ɂ��Ă������̏ꍇ�Ɠ����W��@�������藧���Ƃ𗝉����邱�ƁB -------------------------------- �C�@���̂悤�Ȏv�l�́C���f�́C�\���͓���g�ɕt���邱�ƁB �i��j ��@�y�я��@�̈Ӗ��ɒ��ڂ��C�搔�⏜���������ł���ꍇ�܂Ő��͈̔͂��L���ď�@�y�я��@�̈Ӗ��𑨂������ƂƂ��ɁC�����̌v�Z�̎d�����l������C��������퐶���ɐ��������肷�邱�ƁB |
| ���w�Z�@�w�K�w���v�� �y����z |
�@��S�w�N�ł́C�����̏�@�y�я��@�ɂ��āC���̂܂Ƃ܂�ɒ��ڂ��āC��搔�C�폜���������̏ꍇ�̏�@�⏜�@�C����ʂ̉��{����\���̂ɏ�����p���邱�Ƃ����邱�ƂɊւ��Ďw�����Ă����B -------------------------------- �@��T�w�N�ł́C�搔�C�����������̏ꍇ�ɂ���@�⏜�@���p������悤�ɈӖ����L���邱�Ƃ��˂炢�Ƃ��Ă���B �@���̍ۂɁC�����̏ꍇ�̌v�Z�̈Ӗ���v�Z�̎d�������p���āC�V�����v�Z�̎d�������邱�Ƃ��ł���悤�ɂ��C�w�K�������Ƃ���w�K�Ɋ��p����ԓx��{�����Ƃ���ł���B �@�v�Z�͈̔͂Ƃ��ẮC1/10 �̈ʂ܂ł̏�����1/100 �̈ʂ܂ł̏����Ȃǂ��w������B -------------------------------- �@�����ň琬����鎑���E�\�͂́C�����̏�@�y�я��@�̉��Z�f������C�v�Z�̎d���������������肷��ۂȂǂ̍l�@�ɐ����������̂ł���B |
| �����̏��@�̈Ӗ� |
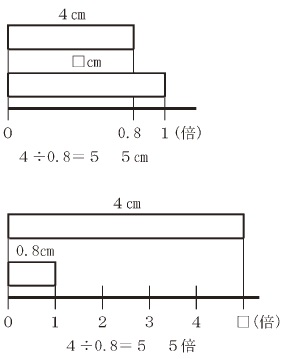
�@���@�̈Ӗ��Ƃ��ẮC �@�a���u��ɂ���傫���v�C -------------------------------- �@ �����`÷�a �@����́C �@�Ⴆ�C �@�u�X���[�g���̐Ԃ����{�����C �@�u�X���[�g���̐Ԃ����{���́C �@�Ƃ����ꍇ�ł���B �@���́C�X÷1.8 �ƂȂ�B -------------------------------- �A �a���`÷�� �@����́C �@�Ⴆ�C �@���́C200÷2.5 �ƂȂ�B -------------------------------- �@�����̎��́C �@���̂Ƃ��C�����̎����ɂƂ��ẮC �@�܂�C �@���̂��Ƃɓ��������B �@���̓_�ɂ��ẮC�����⌾�t�̎������łȂ��C��������}�Ȃǂ�p�������̓I�ȏ�ʂɓ��Ă͂߂��肵�ĕ�����₷�����邱�Ƃ���ł���B �@�܂��C�͂��߂ɏ�@�̎��ɕ\���Ă���C���@�ŋ��߂�Ƃ����l����p���邱�Ƃ���ł���B -------------------------------- �@�Ȃ��C�����Ə��̑傫���̊W�ɂ��ẮC�������P��菬�����Ƃ��C����������ɂȂ鎙���������݂���B �@���̐}�̂悤�Ȑ������Ȃǂ�p����Ȃǂ��āC�������P��菬�����Ƃ��C�����폜�������傫���Ȃ闝�R�ɂ��Đ����ł���悤�ɂ���B
|
| �@ |
| (�) �����̏�@�C���@�̌v�Z |
�@�����́C�����Ɠ����\�i�ʎ��L���@�ŕ\������Ă��邩��C��@�⏜�@�̌v�Z�́C�P�ʁC���Ȃ킿�����_�̈ʒu�ɒ��ڂ��Ă�����ړ����C�����ɒu��������C�����̌v�Z�Ɠ��l�ȍl�����Őς⏤�����߂邱�Ƃ��ł���B �@�\�i�ʎ��L���@�̎d�g�݂��v�Z�ɂ��L���ɐ�������Ă��邱�ƂɋC�t���悤�w�����邱�Ƃ���ł���B -------------------------------- �@�����̏�@�⏜�@�̌v�Z�̎d���́C�v�Z�Ɋւ��Đ��藧������p���āC�����̏�@�⏜�@�ɒ����čl���邱�Ƃ��ł���B -------------------------------- �@�����̏�@�ɂ��ẮC�搔��10�{����Ɛς�10�{�ɂȂ邱�ƂȂǂ̏�@�Ɋւ��Đ��藧���������āC���������K�̐����̏�@�ɒ����čl������悤�ɂ���B �@�Ⴆ�C12×4.3 �̌v�Z�́C �@12×�i4.3×10�j÷10��12×43÷10 �@�ƍl���邱�Ƃ��ł���B �@�܂��C12×0.43 �̌v�Z�́C �@12×�i0.43×100�j÷100��12×43÷100 �@�ƍl���邱�Ƃ��ł���B -------------------------------- �@�����̏��@�ɂ��ẮC�u���@�̌v�Z�ŁC�����y�є폜���ɓ������������Ă����͕ς��Ȃ��v�Ƃ������@�Ɋւ��Đ��藧���������āC�v�Z�̎d�����l������悤�ɂ���B �@�Ⴆ�C7.2÷2.4 �̌v�Z�́C �@�i7.2×10�j÷�i2.4×10�j�� 72÷24 �@�ƍl���邱�Ƃ��ł���B �@�܂��C0.1÷0.04 �̌v�Z�́C �@�i0.1×100�j÷�i0.04×100�j��10÷�S �@�ƍl���邱�Ƃ��ł���B -------------------------------- �@�Ȃ��C����������v�Z�̏�ʂŁC�폜���̍ŏ��̈ʂŊ����Ȃ��Ƃ��́C����i�ނ��Ƃ��ł��邱�Ƃ��w������B �@�Ⴆ�C0.5÷0.4��1.25 �ƂȂ�B -------------------------------- �@�܂��C�����̏��@�ŗ]��̂���ꍇ�́C�]��̏����_�̈ʒu�Ɍ�肪�����̂Œ��ӂ�v����B �@���̍ۂɂ́C�]�肪�\���傫�����l�������C�]��͏�����菬�������Ƃ�C �@�i�폜���j���i�����j×�i���j�{�i�]��j �̎��ɓ��Ă͂߂āC���C�����C�]��̑傫���̊W�𑨂��邱�ƂȂǂɂ��Ďw������B |
| �@ |
| (�) �����̏�@�C���@�̌v�Z |
�@�����̏�@�y�я��@�Ɋւ��Đ��藧�W��@�����C�����̏ꍇ�ł����藧���Ƃ��m���߂�悤�ɂ���B -------------------------------- �@�Ⴆ�C30×2.5 �� 30×�Q�{30×0.5 �����ꂼ��v�Z����ƌ��ʂ͓������Ȃ�B �@��ʂɁC�����̏ꍇ�ł��C �@��×�i���{���j����×���{��×�� �@�Ƃ������z�@�������藧���Ƃ�������B -------------------------------- �@���������v�Z�Ɋւ��Đ��藧���������p���āC�v�Z�̎d�����l������C�v�Z�̌��ʂ��m���߂���ł���悤�ɂ��邱�Ƃ���ł���B |
| �֘A�ꏊ�փW�����v |
| → ���w�Z�Z���� �ڎ� |
| → ���w�Z���w�� �ڎ� |
| → ���w�Z�w�K�w���v�́i2017�j�ڎ� |
| → �w�K�w���v�̃i�r �g�b�v�y�[�W |