|
cosnavi.jp |
| 小学校 学習指導要領 【解説】 |
| 算数編 |
| 第3章 各学年の内容 |
| 第5節 第5学年の目標及び内容 |
| 2 第5学年の内容 |
| 〔数学的活動〕 |
| 小学校 学習指導要領 【本文】 |
(1) 内容の「A数と計算」,「B図形」,「C変化と関係」及び「Dデータの活用」に示す学習については,次のような数学的活動に取り組むものとする。 ア 日常の事象から算数の問題を見いだして解決し,結果を確かめたり,日常生活等に生かしたりする活動 イ 算数の学習場面から算数の問題を見いだして解決し,結果を確かめたり,発展的に考察したりする活動 ウ 問題解決の過程や結果を,図や式などを用いて数学的に表現し伝え合う活動 |
| 小学校 学習指導要領 【解説】 |
それまでの算数の学習経験を踏まえて,児童が目的意識をもって数学的活動に主体的に取り組み,基礎的・基本的な知識及び技能を確実に身に付けるとともに,数学的な思考力,判断力,表現力等を高め,算数に関わりをもったり,算数を学ぶことの楽しさやよさを実感したりできるようにすることを重視する。 -------------------------------- 日常の事象や算数の学習場面から算数の問題を見いだしたり,その解決に既習事項を活用しながら数,式,図やグラフなどの方法を有効に使うなどして思考したり表現したりできるようにする。 -------------------------------- なお,児童の発達の段階を考慮して,これらの数学的活動の視点は前の第4学年と同様の内容とする。 |
データに基づいて身の回りの問題を解決する活動 ~学年とけがの関係の考察~ |
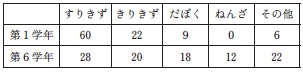
この活動は,「Dデータの活用」の(1)の指導における数学的活動であり,目的に応じてデータを集めて分類整理し,データの特徴や傾向を分析して対策を立てることができるようにすることをねらいとしている。 -------------------------------- 日常生活において,問題に感じることや改善したいことなどに対して,ただ漠然と取り組んでみたり,勘や個人的な経験則を頼りにしたりしていても効果が出ないことがある。 そういった事柄に対しては,データを収集し分析することで実態を的確に把握し,そこから解決策を見いだしたり効果的な対策を講じたりすることができることがある。 -------------------------------- 例えば,小学校のけがについて考察する場面において,児童は次のような数学的活動を遂行とすると考えられる。 -------------------------------- けがについて学習していた際に,「下学年の児童の方が,けがが多そうだ。」という予想をしていたのに,保健だよりなどから,どの学年も同じくらいの人数がけがをしていることを知ったとする。 -------------------------------- そこから 「どの学年も,本当に について調べていく。 けがをした人数が同じくらいであること 第1学年と第6学年のけがの種類(人)
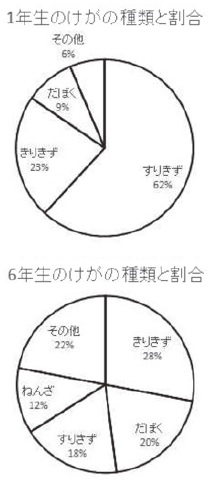
-------------------------------- 学年によって人数が異なるので, そして, 「学年によって, 「けがの種類には,違いがあるのか。」 「けがの程度に違いはあるのか。」 といったような調べる内容を決める。 -------------------------------- どんなデータがあればよいのかを決めれば,次はそのデータを収集する必要がある。 このときどのようにデータを収集するかについても検討できるようにすることが望ましい。 -------------------------------- 収集したデータを分析するため,これまでに学習したような表やグラフにまとめてみる。 観点を二つ取り出して二次元の表に整理することや,その内訳を量的にみるなら棒グラフ,割合でみるなら帯グラフや円グラフというように目的に応じて適切なグラフを選択し表現していく。
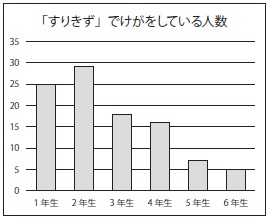
-------------------------------- このとき,全員が同じ観点で分析をしているとは限らない。 むしろ個人やグループごとの関心から様々な分析をしているだろう。 そこで,その結果を交流することで,別の観点から分析した結果を知ることができる。 例えば右のような棒グラフを見ると,1年生がすりきずが多いということだけでなく,下学年ではすりきずが多いという傾向が読み取ることができる。
-------------------------------- このようにして,データを集めて分類整理し,適切な表やグラフを選択して表現し,多面的に捉え考察することで的確な判断が可能となることを学ぶ機会とするのである。 -------------------------------- また,このような活動の方法全体を振り返り,どのようにして結論に至ったかを整理することで,統計的な問題解決の方法を知ることの定着につながると考えられる。 -------------------------------- こうした活動を通じて,自身が問題に感じたことに対して,データを通じて客観的に捉えようとする見方を養い,適切なデータ収集方法や分析の仕方を含めた問題解決の進め方を学び,進んで生活に生かそうとする態度の育成を目指す。 |
乗法の意味を広げる活動 ~乗数が小数の乗法~ |
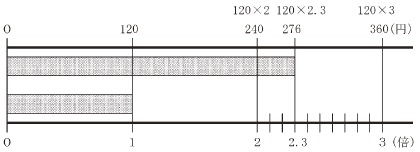
この活動は,「A数と計算」の(3)の指導における数学的活動であり,小数についての既習の内容を根拠に,数直線や図,式などを用いて,乗数が小数についての乗法の意味を見いだすことをねらいとしている。 -------------------------------- 小数の乗法では,乗数が整数のとき乗法の意味を基にして,乗数が小数の場合にも,乗法を用いることができるように意味を広げることを考える。 -------------------------------- 例えば, 「1mのリボンが120円のとき, を考える場面では,
「240円ぐらい。」 「どうして240円だと思ったの。」 「長さが2倍だから, と答える。 -------------------------------- 実際に長さを当てて確かめると, 長さを聞き,2.3mであることを知る。 -------------------------------- そこで,ある児童は, そして, -------------------------------- また,ある児童は, 長さが2倍のときは, 2.3倍という, -------------------------------- これらの考えを伝え合うことで -------------------------------- そこで,児童はそれぞれ, さらに 2倍のところは 120×2 で 240円, ★↑画像をクリックすると拡大します! 「では,2.3倍のところは -------------------------------- そして, 「今までのかけ算は と振り返り, -------------------------------- さらに, -------------------------------- このように,乗数が小数の場合の乗法の意味を,乗数が整数の場合の乗法の意味を基にして,考えられるようにすることが大切である。 |
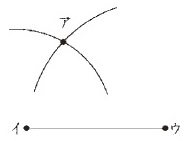
図形を構成する要素に着目して合同な図形の作図の方法を見いだす活動 ~三角形の合同~ |
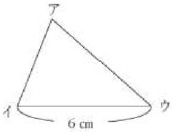
この活動は,「B図形」の(1)の指導における数学的活動であり,図形を構成する要素に着目し,合同な図形をかく活動を通して,どの構成要素が決まれば図形の形や大きさが一つに決定するかという図形の決定条件を考えることをねらいとするものである。 -------------------------------- ここでは,ぴったり重なるという具体的な操作を,対応する辺の長さや角の大きさが等しいかどうかに置き換えて考えていくことになる。 -------------------------------- 例えば,辺イウの長さが6㎝であることのみを示した右のような三角形アイウを基に
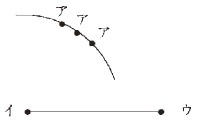
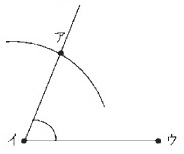
「この三角形と合同な三角形 という問題の場面では -------------------------------- 「合同な図形は,全ての対応する辺の長さと角の大きさが等しかったから,辺の長さや角の大きさが知りたい。」 「でも,全ての辺の長さや角の大きさを調べる必要があるのだろうか。」 と話し合ったり, 「辺イウが決まったということは,三角形の三つの頂点のうち,二つが決まったということだ。」 と考えを進めたりする中で, 「あと一つの頂点アの位置を決めるには,何を調べたらよいだろう。」 と問題を焦点化していくだろう。 -------------------------------- 例えば,まず,
頂点アの位置が決まらない。 角イの大きさを調べると,
-------------------------------- 辺アウの長さを調べると,
-------------------------------- このように調べていくことを通して,三つの構成要素をうまく選ぶと,三角形が一つに決定することに気付いていく。 -------------------------------- そして,ほかに調べた児童と交流し,三角形が決まる条件はほかにもあるがそれをもとにすると,合同な三角形を書くことができることを見いだしていく。 -------------------------------- 「正三角形や二等辺三角形の場合は, 「四角形の場合は,どうだろう。」 などと別の図形について発展的に考えることも考えられる。 新たな図形を考察する観点を学んだら,その観点で既習の図形について見直そうとする態度が育成されることも大切である。 |
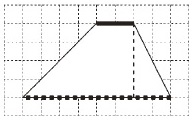
図形の特徴や図形を構成する要素に着目して面積の求め方を考察する活動 ~台形の面積の公式作り~ |
この活動は,「B図形」の(3)の指導における数学的活動であり,図形の特徴や図形を構成する要素に着目して,図形の面積の求め方を考え,図と式を関連付けて説明することを通して,問題解決の過程や結果を数学的に表現する力を高めることをねらいとしている。 -------------------------------- これまでに,児童は,正方形や長方形の面積の求め方について,辺の長さに着目し,計算によって面積を求めることのよさに気付き,図形を構成する要素である辺に着目することで面積の公式を作ることを考えてきている。 第5学年では,これらの経験を踏まえて,図形の見方や既習の面積を求める公式の作り方を活用し,三角形や平行四辺形,台形及びひし形の面積の求め方を工夫して考え,その考え方を公式へと表現を高めていく。 -------------------------------- 例えば,右の図のような 上底が2㎝,下底が8㎝,
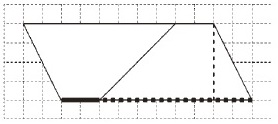
の面積を求め方を考えたことを基に, -------------------------------- 台形の面積の求め方として, 「台形を二つ合わせて
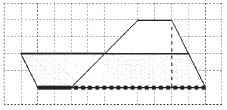
「台形を横に切って
などのように考えたことを伝え合い, -------------------------------- そこで,これらの活動を振り返り,面積の公式を知っている図形に台形を変形したことから,台形の面積が求められたことをまとめる。 -------------------------------- ここでさらに,三角形や平行四辺形と同じように「台形も公式があるといいのではないか。台形の公式を考えよう。」という問いをもつことが考えられる。 -------------------------------- そこでまず,平行四辺形や三角形のとき,どのように公式を作ったのかを振り返る。 ① 面積を計算した図形の辺や高さなどが,もとの図形の辺や高さなどに当たるかを捉える。 ② 数値を用語に置き換え,言葉の式に表す。 ③ 幾つかの考えの共通点を見付けて公式にする。 -------------------------------- そこで,このことを基に台形の公式を作っていく。 -------------------------------- 台形を二つ合わせて平行四辺形にする考えでは,次のように考えるだろう。 ★↑画像をクリックすると拡大します! このことから -------------------------------- また,台形を横に切って一部を移動して平行四辺形にする考えでは,次のように考えるだろう。 ★↑画像をクリックすると拡大します! このことからも -------------------------------- このように どの求め方からも -------------------------------- これらの経験を通して,図と式を関連付けて考える力や,式に表現したことを公式という簡潔・明瞭・的確な表現に高めていく力の育成を目指す。 |
| 関連場所へジャンプ |
| → 小学校算数編 目次 |
| → 中学校数学編 目次 |
| → 小学校学習指導要領(2017)目次 |
| → 学習指導要領ナビ トップページ |